Analytic Function Visualization

This webapp is a somewhat-naive tool to visualize complex, and, in particular, complex-analytic functions. You can enter a function in the very top left; the left half shows $\mathbb C$ and the right half shows the image of $\mathbb C$ under the given function.

But what's with those two circles in the domain and codomain?

The circles have to do with complex-analytic functions. The idea of a function being 'analytic' may be thought of as it being 'locally a dilation and rotation'. That is, if we zoom in really close to a neighborhood around a point, and look at the image of that neighborhood under the function, the latter will look like a rotation and scaling of the former. The circles are used to visualize that rotation and scaling.

It is important to note that the center of the rotation and dilation is not zero but rather the center of a neighborhood.

Woah, slow down. Hold up. From the beginning.

We have a function $f : \mathbb C \to \mathbb C$. Let's take a look at a single point in $\mathbb C$, call it $z_0$. Consider some small movement or "arrow" $\Delta z$ within the domain that will take $z_0$ to $z_0 + \Delta z$. If we consider the image of $z_0$ and $z_0 + \Delta z$, which are $f(z_0)$ and $f(z_0 + \Delta z)$, respectively, we may draw another arrow, analogous to the $\Delta z$ arrow, between them which represents the movement it would take to bring $f(z_0)$ to $f(z_0 + \Delta z)$. The size of this second arrow is $f(z_0 + \Delta z) - f(z_0)$.

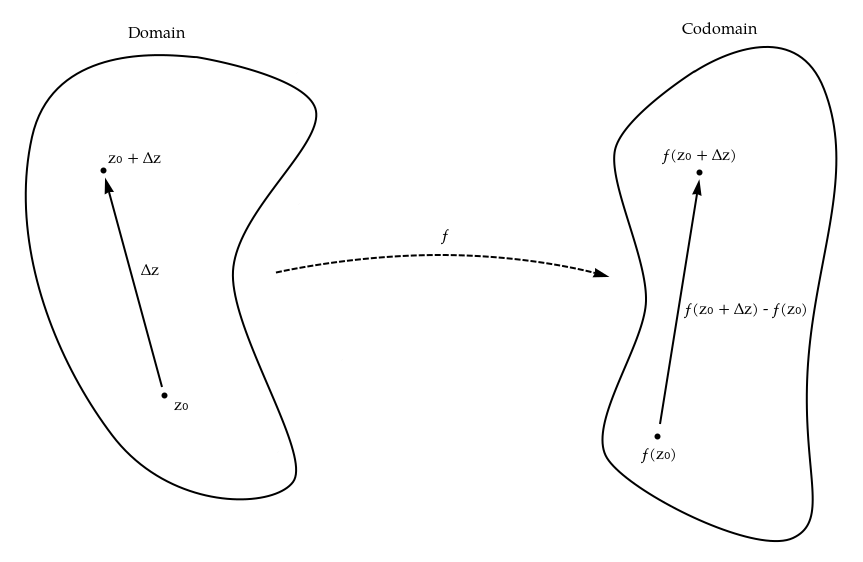
But what's this got to do with analyticity? A function is analytic iff it is differentiable. And it is differentiable if its derivative exists, i.e.,

It's actually slightly subtler than this, since a function may be differentiable at a point but may only be analytic on an open set.

$$ \exists f'(z_0) := \lim_{\Delta z \to 0} \frac{f(z_0 + \Delta z) - f(z_0)}{\Delta z} $$

Hey, those symbols look familiar! You may see where this is going. Limits are beautiful and rigorous things, but we are going to be naughty and rewrite this statement as:

$$ f'(z_0) \approx \frac{f(z_0 + \Delta z) - f(z_0)}{\Delta z} $$

and then multiply by $\Delta z$, giving:

$$ f'(z_0) \cdot \Delta z \approx f(z_0 + \Delta z) - f(z_0) $$

In the context of the figure, this says that the two arrows, one in the domain and one in the codomain, are (approximately) multiples of each other. In particular, the multiple is $f'(z_0)$.

The rigorous version is that in the limit case, the two arrows are multiples of each other.

Since $\Delta z$ is arbitrary, we may point the domain arrow in any direction and give it any magnitude, and the corresponding arrow in the image will still be a multiple of it. In fact, since this multiple is $f'(z_0)$, which is independent of $\Delta z$, it's the same multiple for every arrow we draw.

This means that we could instead draw a circle in the domain, and the corresponding circle in the image could also be approximated as a multiple of the domain's circle. This is what the circles are. They are a way of visualizing the local rotation and scaling of the function. A circle is drawn in the domain, centered around $z_0$, and drawn, rotated and scaled by $f'(z_0)$, in the codomain, centered around $f(z_0)$.

The size of the circle may be changed in the settings menu, but not that it's called $\epsilon$ rather than $\Delta z$.