I'd like to share with you an interesting problem I ran across when working a project for my graphics class.
In the class, we've been coding simple object rendering. We started with 2D, drawing simple colored polygons:

A colored polygon
and then we allowed the user to clip said polygons:
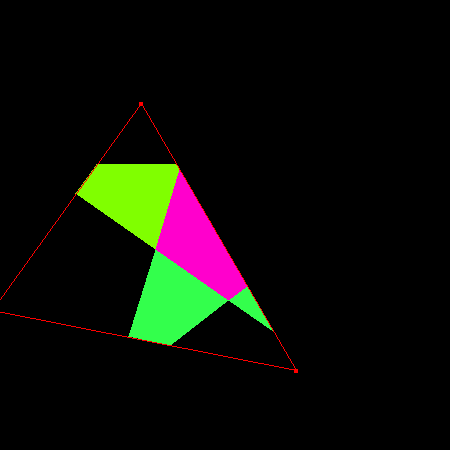
A clipped polygon
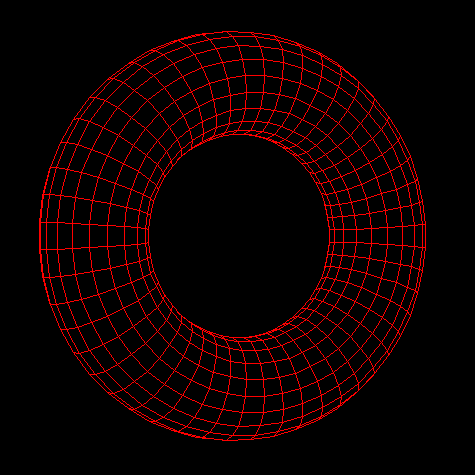
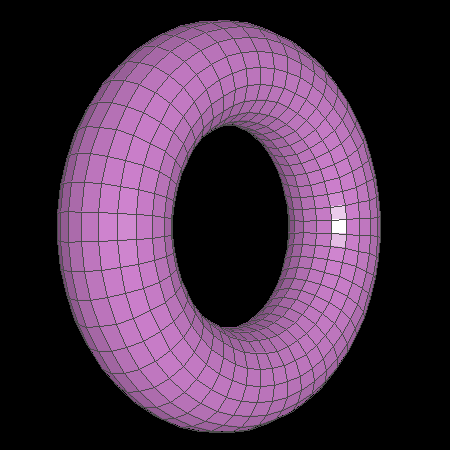
And then we moved onto 3D! This started out with rendering simple wireframes, for instance of this torus:

A torus displayed as a 3d wireframe
We then implemented an improvement called "backface elimination" which improves rendering of some shapes, including this torus ...
Backface elimination removes the 'back' of the torus
... but only from certain angles ...

Backface elimination does not work perfectly on a torus
Then we actually filled in the polygons instead of just painting their wireframes:
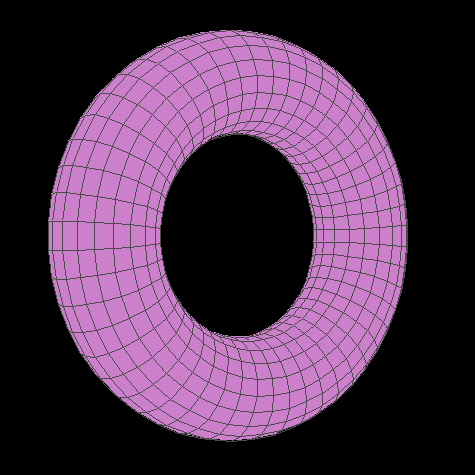
A painted torus
Actually, I'm not sure where exactly this came in the timeline. It's not important.
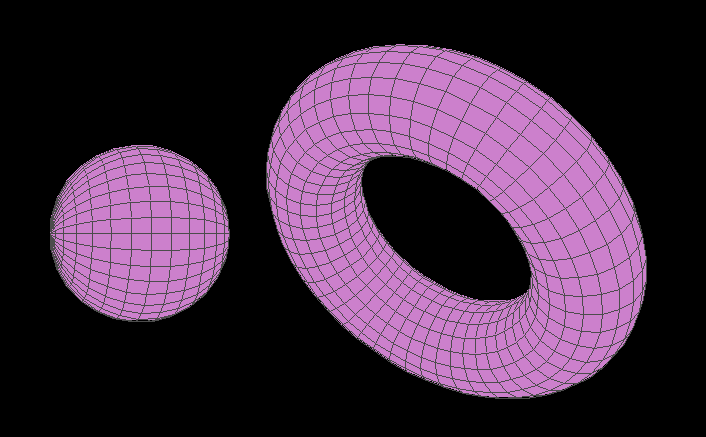
A painted torus next to a painted sphere
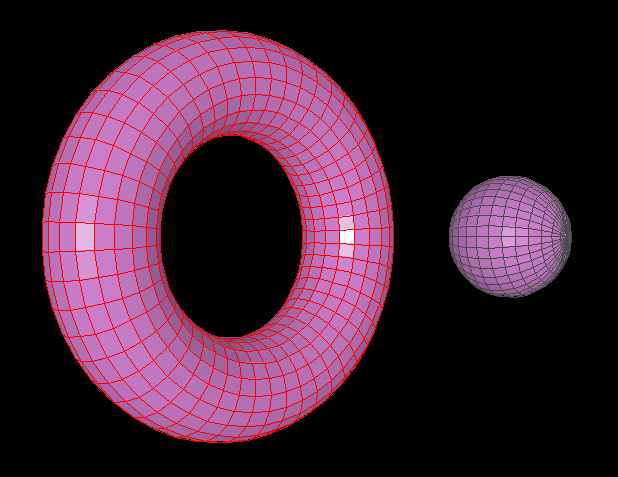
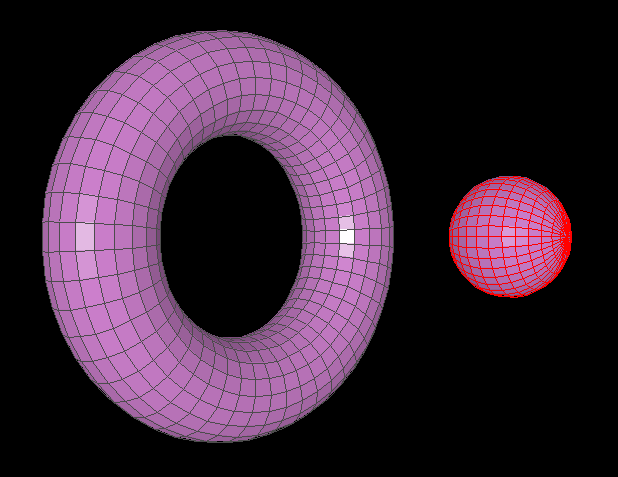
Then we added lighting!
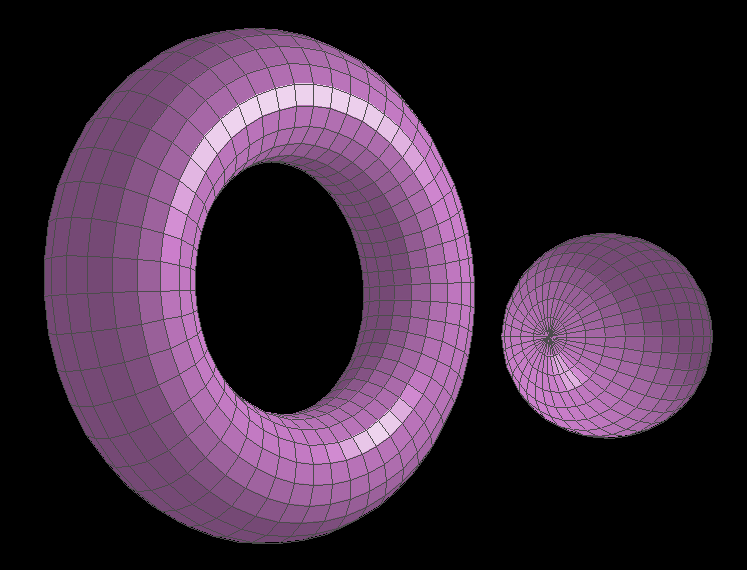
A torus next to a sphere, both lit
This is actually a slight lie: I accounted for intersections before doing lighting. But this order works better for the blog post.

A torus and sphere intersecting
The problem of how to allow for intersections like this is actually a bit subtle.
See, the naive rendering implementation is just to render objects back-to-front. Take a list of objects, sort it by distance to observer, and draw the objects, farthest-to-closest. In order to do the sort, we would call qsort with a comparator function which compares two object and tells qsort which one should come before the other in the list.
This comparator would look
... except written in C, not pseudo-JS.
function comparator(object1, object2) {
// Order by distance
let distance1 = distance_to_observer(object1);
let distance2 = distance_to_observer(object2);
if (distance1 > distance2) return PAINT_OBJECT1_FIRST;
if (distance2 > distance1) return PAINT_OBJECT2_FIRST;
return PAINT_EITHER_FIRST;
}
However, this cannot render any intersections, since each objects is rendered wholesale, one-at-a-time.
Instead, a better approach is to decompose all objects into their constituent polygons, collect them all in an aggregate list, sort this by distance to observer, and paint each polygon one-at-a-time. So that's what I did. The comparator looked the same as the previous one, but as a function of polygons instead of objects:
function comparator(poly1, poly2) {
// Order by distance
let distance1 = distance_to_observer(poly1);
let distance2 = distance_to_observer(poly2);
if (distance1 > distance2) return PAINT_POLY1_FIRST;
if (distance2 > distance1) return PAINT_POLY2_FIRST;
return PAINT_EITHER_FIRST;
}
And it worked great! (As is evident by the existence of the photo in which clipping is working correctly)
Now is where things start getting funky. See, the user was able to manipulate one object at a time with the keyboard. I visually cued which object was selected by changing the color of its wireframe:
Selection was cued by a change of wireframe color
but I wasn't happy with this (for a few reasons). Instead, I wanted to do something cooler: I wanted to draw a halo around whichever object was selected:
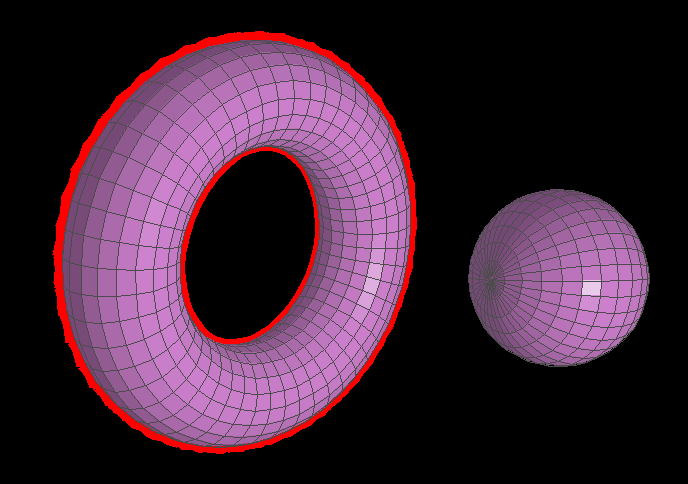
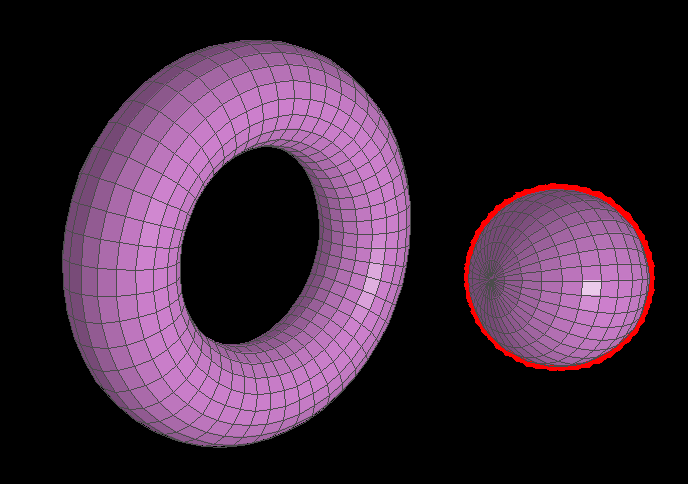
Cuing selection with a halo instead
Looking at the above images, you may think I succeeded in doing so. And I did! Kind of. With those specific objects in those specific positions with those specific angles, the halos render correctly. In general, however, they don't. As it turns out, the problem of how to render these halos is quite tricky...
So how did I render the halos?
The pieces of the algorithm relevant to halo rendering are creating and sorting the list of polygons. Firstly, besides adding each polygon into an aggregate list like we were before, we also add extra polygons:
Another option is to dilate the object as a whole around its center; however, this has some issues. It would work perfectly on a sphere but wouldn't work as well on a torus: the inside of the torus would get no halo.
The question, then, is how exactly to sort the list of polygons. We want red behind purple, of course, but code demands we be more precise.
Another option is to paint all red polygons before all purple polygons, and otherwise paint by distance:
function comparator(poly1, poly2) {
// Place red before purple
if (is_red(poly1) && !is_red(poly2)) return PAINT_POLY1_FIRST;
if (is_red(poly2) && !is_red(poly1)) return PAINT_POLY2_FIRST;
// Otherwise, order by distance
let distance1 = distance_to_observer(poly1);
let distance2 = distance_to_observer(poly2);
if (distance1 > distance2) return PAINT_POLY1_FIRST;
if (distance2 > distance1) return PAINT_POLY2_FIRST;
return PAINT_EITHER_FIRST;
}
The issue with this is that it means that the halo is never painted on top of anything else. However, it is sometimes appropriate to paint the halo on top of other things. For instance, if a selected torus is entirely in front of a sphere, it would make sense for the halo to be painted on top of the sphere.
function comparator(poly1, poly2) {
// Order by distance
let distance1 = distance_to_observer(poly1);
let distance2 = distance_to_observer(poly2);
if (distance1 > distance2) return PAINT_POLY1_FIRST;
if (distance2 > distance1) return PAINT_POLY2_FIRST;
// If the same distance, for instance in the case of a pair
// of buddy red and purple polygons, paint the red polygon first
if (is_red(poly1) && !is_red(poly2)) return PAINT_POLY1_FIRST;
if (is_red(poly2) && !is_red(poly1)) return PAINT_POLY2_FIRST;
return PAINT_EITHER_FIRST;
}
...unfortunately, this doesn't work so well:

The naive comparator algorithm does not work well
The issue is that since each red polygon is enlarged, it obscures all the purple polygons behind it. Thus, the only purple polygon you're able to see is the one in the very front.
Okay, let's try again. In order to avoid the previous problem, we'll place each red polygon behind all polygons from the focused model. Otherwise, we'll paint in order of decreasing distance, just as before:
function comparator(poly1, poly2) {
// If both polygons are from the focused model
/// (they can be either red or purple)
if (is_in_focused_polygon(poly1) && is_in_focused_polygon(poly2)) {
// Paint red polygons first
if (is_red(poly1) && !is_red(poly2)) return PAINT_POLY1_FIRST;
if (is_red(poly2) && !is_red(poly1)) return PAINT_POLY2_FIRST;
}
// Otherwise, order by distance
let distance1 = distance_to_observer(poly1);
let distance2 = distance_to_observer(poly2);
if (distance1 > distance2) return PAINT_POLY1_FIRST;
if (distance2 > distance1) return PAINT_POLY2_FIRST;
return PAINT_EITHER_FIRST;
}
Deviously, this one
In fact, it's the comparator function I used to generate the original "correct" halo images.
For instance, sometimes polygons render out-of-order or don't render at all, causing glitchy holes and red blotches on the torus:
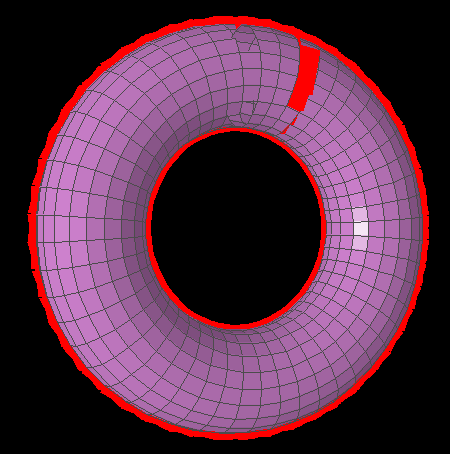

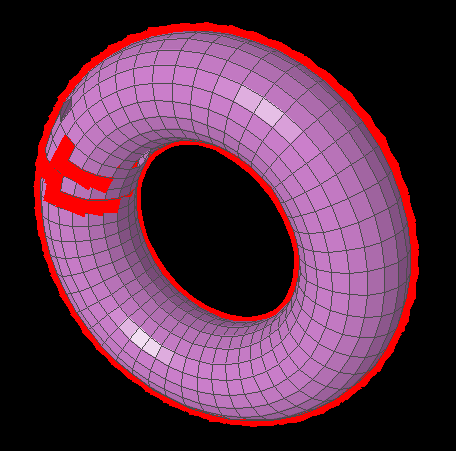
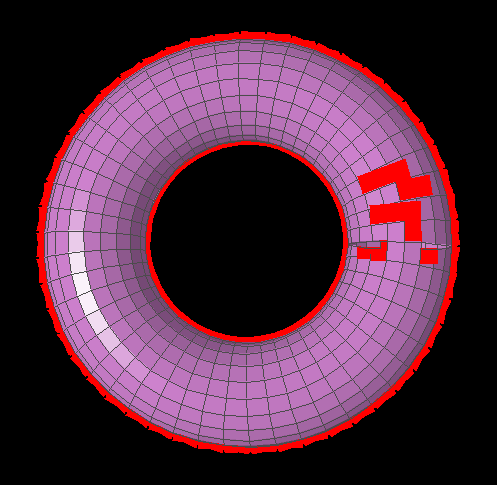
With this comparator, some polygons are rendered out of order or not at all
Even weirder, I found a setup with a torus and a sphere in which the torus would render differently based on how the sphere was rotated:
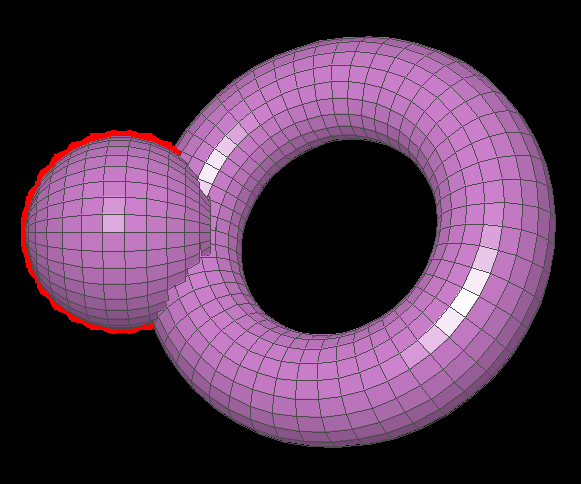
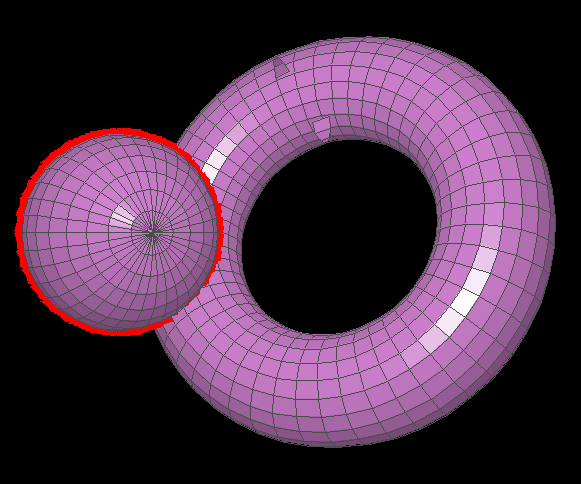
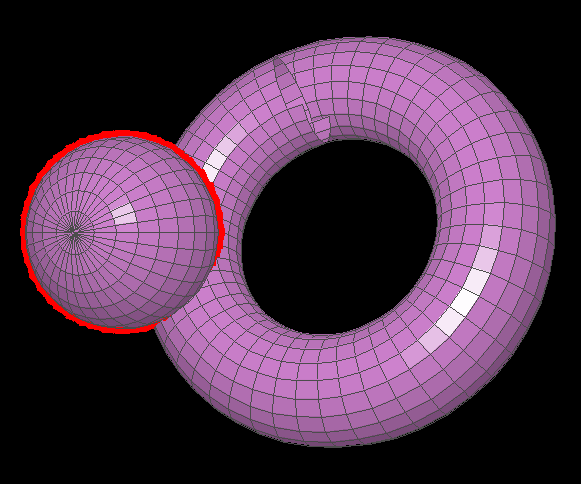
As the sphere is rotated, polygons on the top of the torus begin to render incorrectly
So what the hell is going on?
Consider more weird behavior in which the apparent overlapping of two objects will depend on which object is selected:
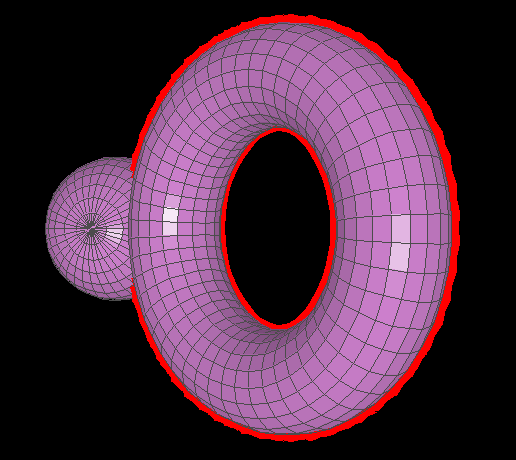
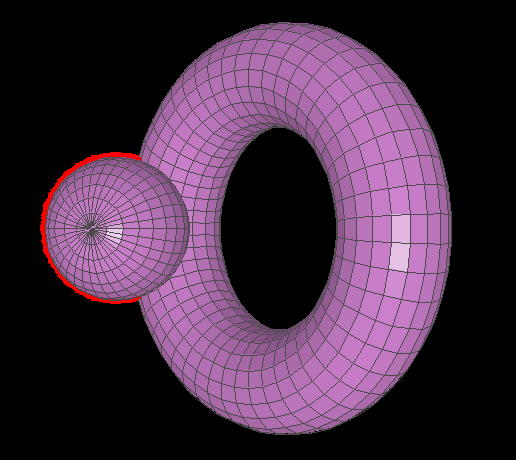
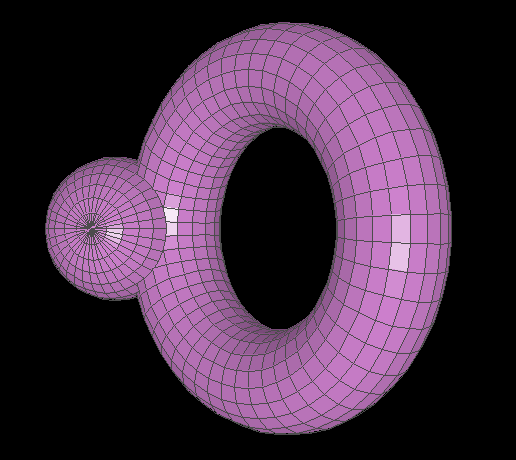
The object that appears 'on top' depends on which object is selected (either way, the halo appears 'behind')
In actuality, the sphere is clipping into the torus (as can be seen by the third image, where nothing is selected). However, when the torus is selected, the way comparator is defined allows us to prove that it should be drawn entirely on top of the sphere.
To show you why, let's label some points:
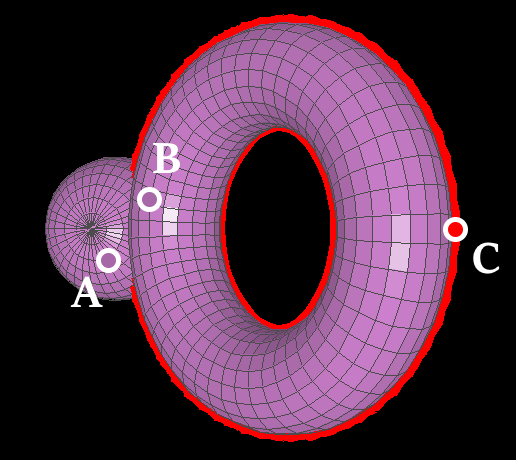
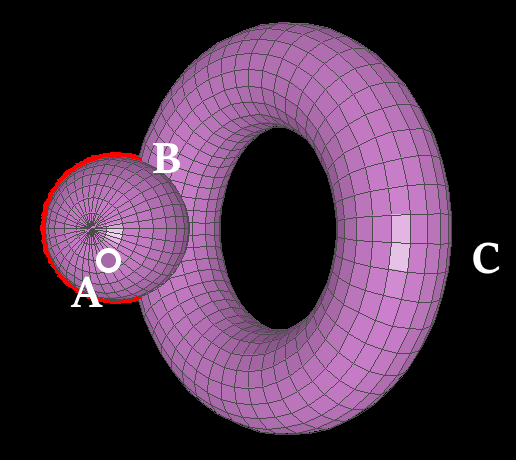
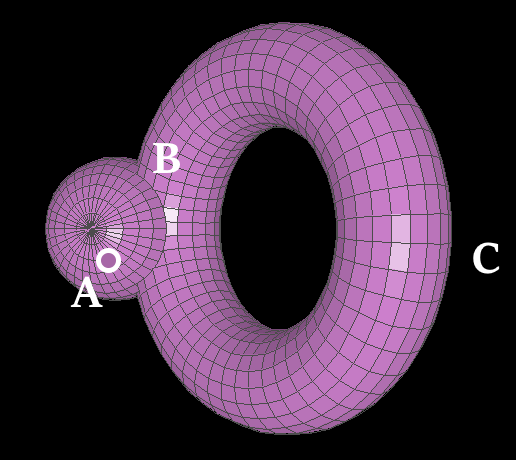
Labelings of three choice points. Labels are always shown, but dots are only visible when the points they represent are visible. $A$ is on the sphere, $B$ is on the torus, and $C$ is on the torus' halo. Since $B$ is behind the sphere (see image 3), we know that $A$ is closer to the observer than $B$.
I will use the notation $X \rightharpoonup Y$ to mean that comparator tells us to paint $Y$ after $X$. The arrow points from painted first to painted last, from painted on the bottom to painted on the top. It may be pronounced "before" or "and then" or "under".
Now I will show that, strangely, $A \rightharpoonup B$ despite $B$ being further from the observer:
comparator tells us to paint $C$ before $B$, i.e. $C \rightharpoonup B$.comparator tells us that $A$ should be painted under $C$, aka that $A \rightharpoonup C$.In this manner we are able to show that, if the torus is selected, then comparator tells us to paint $A$ before $B$. A similar proof may be repeated for all the pounts near $B$ on the torus, thus painting the torus entirely on top of the sphere.
When the sphere is selected instead of the torus, we are able to do similar proofs for its polygons, showing that the sphere is visually on top of the torus.
I conjecture that qsort is doing
Note we can also prove that the sphere polygon should be painted before the purple polygon, since they are from different polygons and the sphere polygon is further than the purple polygon. Thus, the sphere polygon should be painted before the torus polygon, but also, as we have already shown, the torus polygon should be painted before the sphere polygon. Impossible!
I think (but have not proven) that you can (constructively, without use of LEM) prove, for any two polygons $a$ and $b$, that $a$ should be painted before $b$.
So what's going wrong here? Where's the mistake in these proofs?
The issue is that we're treating comparator as something it isn't. In particular, in our proof we assume the transitivity of $\rightharpoonup$, that if comparator it places $a$ before $b$ in the paint order (i.e. $a \rightharpoonup b$), and placed $b$ before $c$ (i.e. $b \rightharpoonup c$), then it will also place $a$ before $c$ (i.e. $a \rightharpoonup c$). But this simply isn't true!
This corresponds to the qsort expects comparator to represent a total ordering—i.e., be sufficiently nice and sufficiently self-consistent in certain ways, such as transitivity—but the comparator we wrote does not represent a total ordering.
I actually haven't verified this, but I can't imagine that it isn't true.
So how did I fix comparator? Well, I didn't! I'm still not sure about a good solution to this issue. If you have any ideas, let me know! I hope you thought this was as interesting as I did!